목차
1. 서론
2. FCN 구조
2.1. Convolutionalization
2.2. Upsampling
2.3. Skip connection
3. Other details
4. FCN 수식 정의
1. 서론
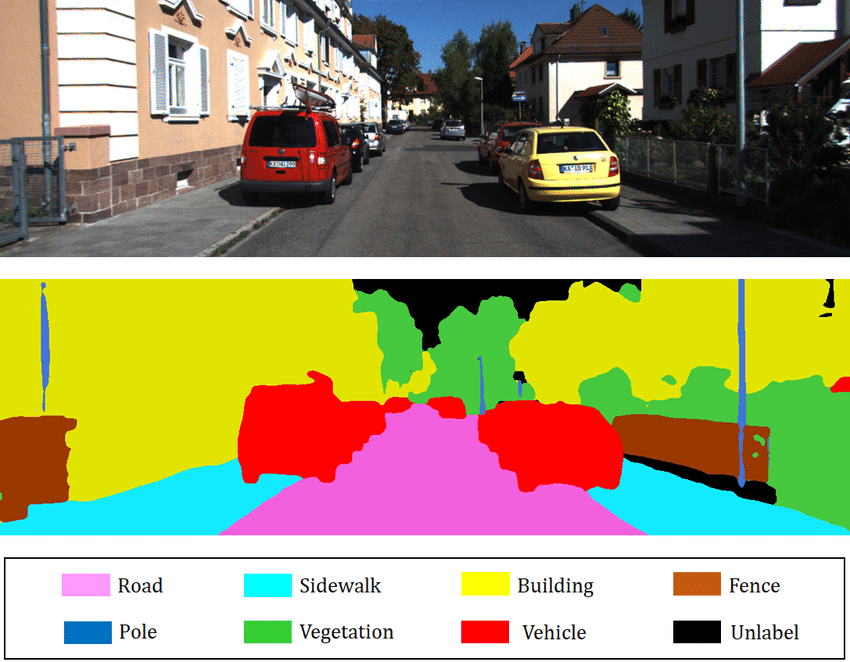
Fully Convolutional Networks for Semantic Segmentation 논문은 2015년 기준 새로운 시멘틱 세그멘테이션(Semantic Segmentation) 방법에 대해 설명한다. Semantic Segmentation을 번역하면 "의미적 분할" 정도일 것이다. 다소 어색하게 느껴지지만 이미지를 의미 있는 단위로 나눈다는 말이다. 시멘틱 세그멘테이션을 적용하면 이미지의 영역마다 무엇이 있는지 알 수 있다. 그림1은 주택가 사진을 시멘틱 세그멘테이션한 결과를 보여준다. 빨간색 부분은 자동차, 보라색 부분은 도로, 하늘색 부분은 인도를 '의미'한다. 단, 시멘틱 세그멘테이션에서는 차량은 모두 빨간색으로 색칠되어 개별 차량을 구분할 수는 없는데, 차량(클래스)별로도 빨간 차, 노란 차 등(인스턴스)을 구분하는 것은 인스턴스 세그멘테이션(instance segmentation)이다.
Fully Convolutional Network(FCN) 이후 거의 모든 시멘틱 세그멘테이션 연구는 FCN을 기반으로 한다. 다시 말해, FCN이 시멘틱 세그멘테이션의 새로운 연구 방향을 제시했다고 할 수 있다. 기존의 이미지 분류 모델은 이미지 하나의 클래스를 분류했다. 시멘틱 세그멘테이션은 픽셀마다 어떤 클래스에 속하는지 분류해야 한다. 픽셀 단위의 분류를 위해서 FCN은 합성곱층(convolutional layer)으로만 신경망을 구성한다. FCN의 중요한 특징은 정확한 위치 추론(Localization)을 위해서 다양한 스케일의 특징맵을 이용한다는 것이다.
2. FCN 구조
2.1. Convolutionalization
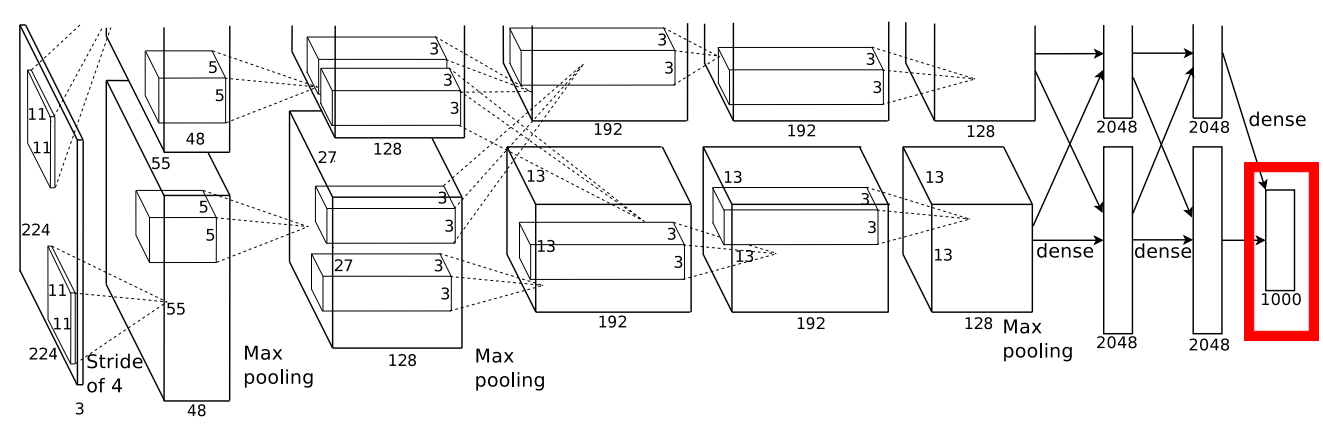


CNN(합성곱 신경망; Convolutional Neural Network)을 이용한 이미지 분류 모델은 끝단에 완전결합층(fully-connected layer)으로 구성된 분류기(Classifier)를 이용한다. 그림 3, 4, 5는 각각 ILSVRC(ImageNet Large Scale Visual Recognition Challenge) 대회에서 2012년도 우승, 2014년도 우승, 준우승을 차지한 AlexNet, GoogleNet, VGG-16의 아키텍처다. 세 모델에서도 이미지 분류를 위해 완전결합층(빨간 박스)를 사용한 것을 볼 수 있다.
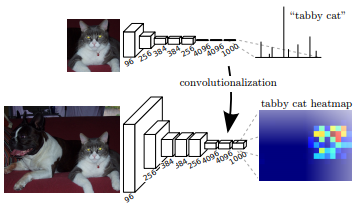
FCN은 새로운 모델을 설계하지 않고, 다른 이미지 분류 모델을 이용해 미세 조정(fine-tuning)한다. CNN의 파라미터는 기존에 학습된 채로 고정한 후, 분류기만 새로운 데이터셋에 맞춰 학습하는 것이다. 이때 분류기를 그대로 사용하지 않는다. 시멘틱 세그멘테이션을 위해서는 네트워크의 결과가 3D 형상이어야 한다. 하지만 기존 분류기의 완전결합층 결과는 1D 형상이다. 따라서 분류기의 완전결합층을 합성곱층으로 바꿔 3D 특징맵을 산출한다. 논문에서는 이렇게 분류기를 수정하는 과정을 Convolutionalization이라고 한다. 그림 6은 AlexNet의 분류기를 합성곱층으로 만드는 과정을 보여준다.
분류기를 합성곱층으로 바꾸는 과정을 자세히 살펴보자. AlexNet의 분류기를 수정할 때 마지막 단의 완전 결합층을 필터의 크기가 1x1인 합성곱층으로 대체한다. 기존 recognition 모델의 마지막 FC에서는 1000개의 클래스에 맞춰 노드의 수가 1000개였다면, Fine-tune 된 마지막 Convnet은 채널 수를 클래스 수에 맞춰 1000개로 구성한다. 그러면 각 채널별 feature 맵은 한 클래스(고양이)에 대한 히트맵이 된다. Figure2에서 확인할 수 있듯이 FC를 Convolutionalize하는 것으로 결과값이 Prediction Scores(Non-spatial output)에서 히트맵(Spatial output)으로 바뀌었다. 히트맵을 통해서 이미지 어디쯤에 고양이가 위치하는지 알 수 있다. 하지만 Figure 2의 히트맵은 픽셀수가 굉장히 적고 정확하고 충분한 정보를 담고 있다고 보기 어렵다. 이 문제를 해결하기 위해서 FCN의 마지막에 Feature map을 Upsample해 output size를 input size와 같게 만든다. 그리고 최종 Output을 Upsample한 것만으로는 성능이 좋지 않아 Skip Architecture라는 새로운 방법을 사용한다.
. (feature representation)을 이용할 수 있고, 학습 시간이 얼마 들지 않는다는 장점이 있다. 본 논문에서는 AlexNet, GoogleNet, VGGNet을 Fine-Tuning했다.

3. Rely on Upsampling
Figure 2의 히트맵의 픽셀 수는 Input이미지의 픽셀 수보다 매우 적다. Convnet은 기본적으로 입력 이미지를 Downsampling하기 때문이다(커널 사이즈와 스트라이드에 비례해서 패딩하지 않거나 pooling을 사용한다면). 따라서 Convnet만 이용해서는 최종 히트맵은 정확히 고양이가 위치한 픽셀을 원본 이미지 사이즈로 표현할 수 없다.
픽셀 단위 예측(pixel-wise prediction)을 위해서는 Output의 크기가 Input의 크기와 동일해야 한다. 본 논문에서는 작아진 feature map(앞서 말한 히트맵)을 input size와 동일하게 키우기 위해서 마지막에 Upsampling layer를 추가한다. 아래 Figure1에서 feature map의 사이즈가 계속 작아지다가 마지막에 input 사이즈와 동일하게 커지는 것을 볼 수 있다. 참고로, figure 1의 pixelwise prediction layer는 PASCAL 데이터셋의 21개의 클래스에 맞춰 마지막 layer의 channel 수가 21인 것을 볼 수 있다.

Upsampling은 Pooling같은 Downsampling과 반대로 해상도(픽셀 수)를 높이는, 즉 이미지를 크게 만드는 작업이다. Upsampling에는 Nearest Neighbors, Bed of Nails, max-unpooling, Interpolation, transposed convolution (deconvolution) 등 다양한 방법이 있다. FCN에서는 Upsampling 방법으로 Deconvolution을 이용 한다. Deconvolution은 Convolution과 마찬가지로 kernel(filter)를 이용해 연산하는데, kernel parameter를 학습할 수 있다. 아래는 논문의 VGG-16s 공식 구현 코드 발췌부분이다. 이 구조에서는 2배, 16배 upsample을 이용한다.
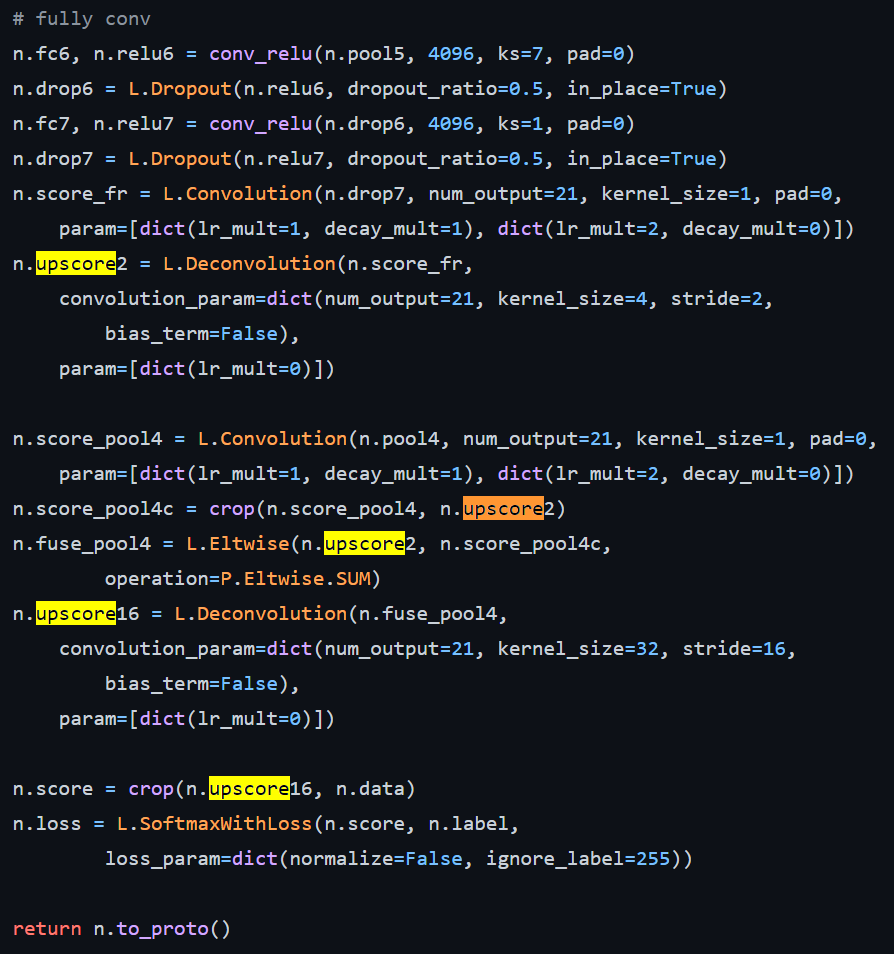


논문에서 2배 Deconvolution filter는 bilinear interpolation으로 초기화한다. 이 말은 deconvolution결과가 bilinear interpolation 결과와 동일하도록 kernel parameter을 초기화하는 것으로 보인다. 그리고 학습률(lr_mult)를 0으로 설정해 kernel을 학습하지 않고 고정시켰다.
논문에서는 16배 Upsample의 parameter를 모두 0으로 초기화하고 학습률은 100만큼 줄인다고 한다. 하지만 실제 코드에서 upscore16 layer의 학습률(lr_mult)가 0인데, 이렇게 되면 0으로 초기화된 값이 update되지 않기 때문에 제대로 학습되지 않을 듯 하다.
Bilinear Interpolation
Bilinear Interpolation은 다크프로그래머님의 블로그 내용으로 대체한다.
Deconvolution
deconvolution은 convolution을 역으로 연산하는 듯하다 해서 backward strided convolution이라고도 불리고, forward에 사용했던 filter를 transpose해서 사용하기 때문에 transposed convolution이라고도 한다. 이외에도 다양한 용어로 사용되기도 하는데, FCN 논문에서 사용하는 deconvolution으로 설명을 이어가도록 하겠다. 아래의 설명과 그림은 이 블로그를 참고했다.
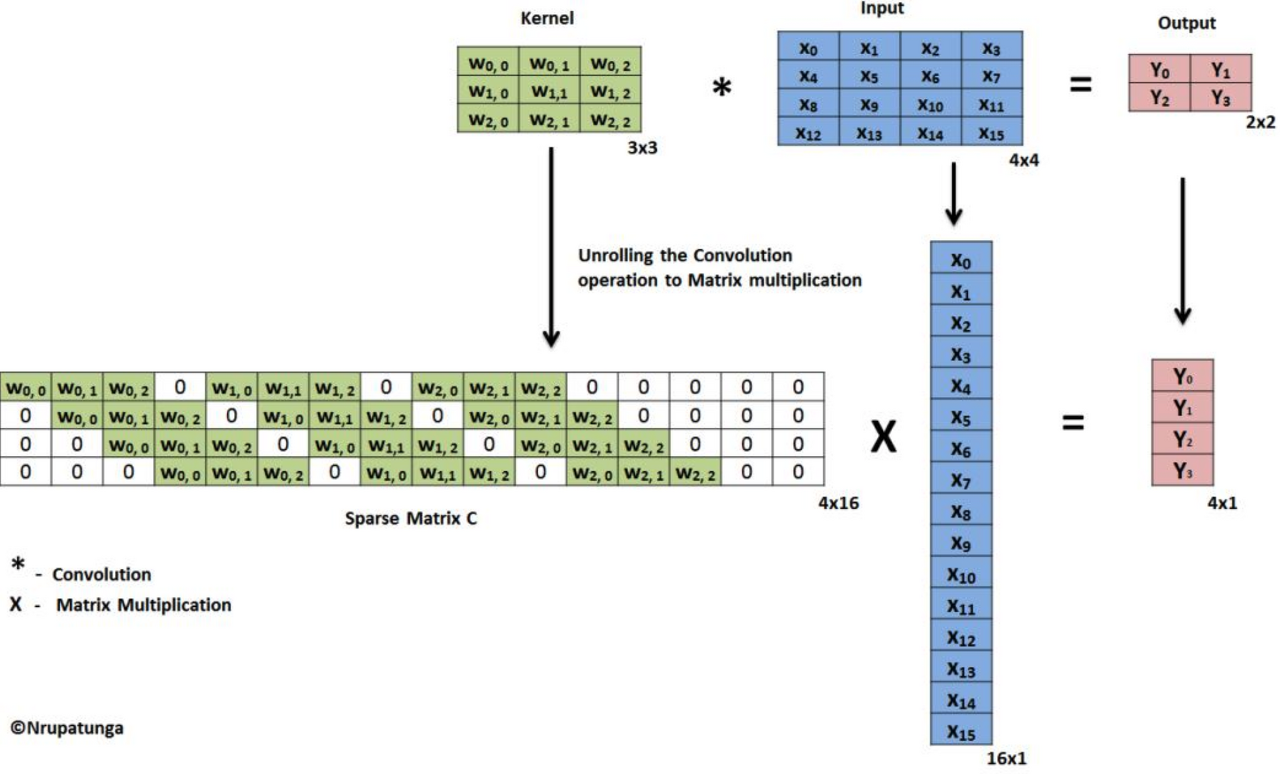
위 그림은 일반적인 convolution 연산을 행렬 연산으로 표현한 것이다. kernel, input, output 형상은 아래 보이는 대로고 stride는 1이다.
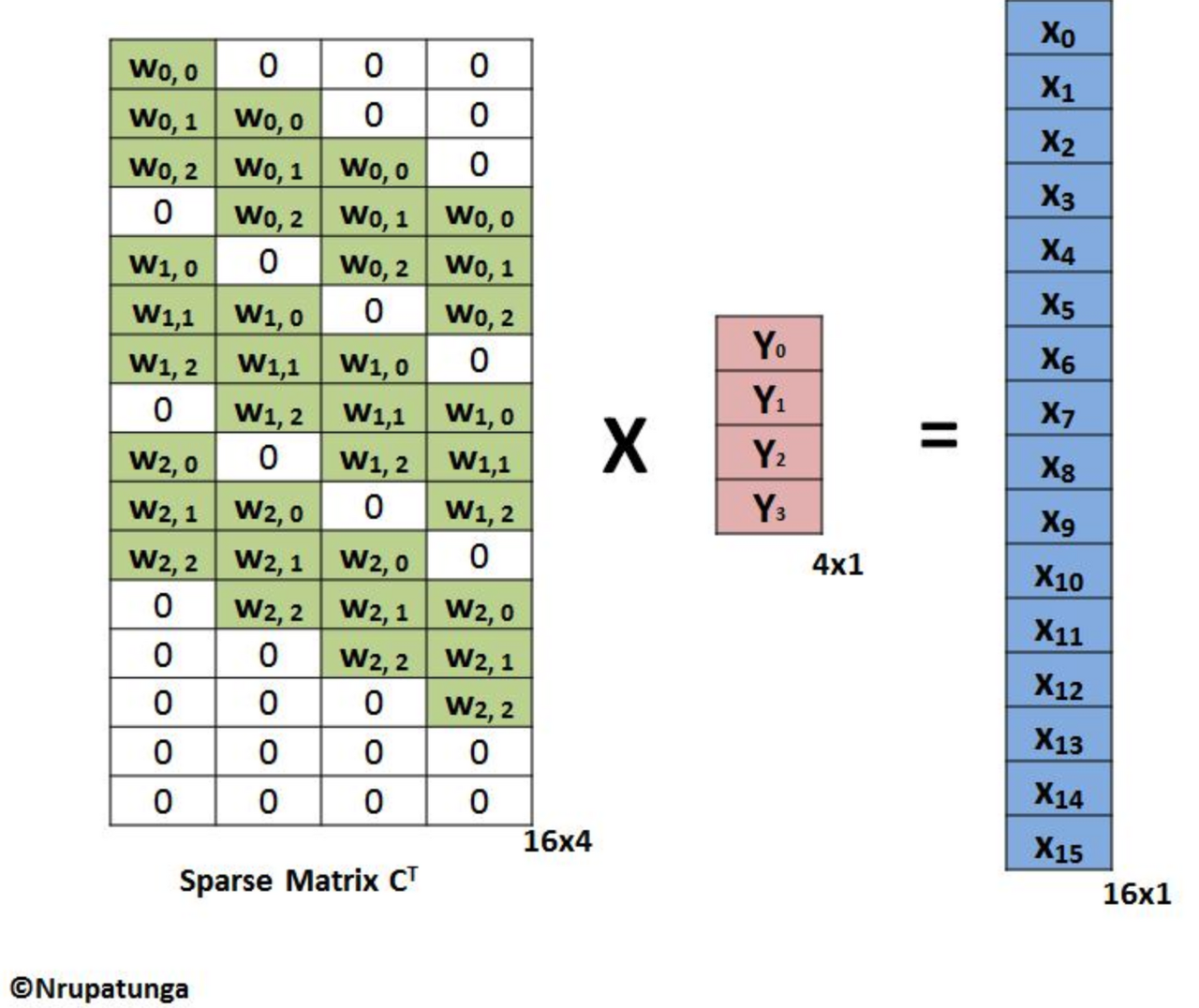
Convolution 수식을 간단히 C(kernel) x X(Input) = Y(Output)라고 하자. C는 4x16, X는 16x1 형상이기 때문에 Output은 4x1이 되고, 이를 reshape해서 2x2 Output을 얻어낼 수 있다. deconvolution의 목적은 2x2 Y행렬을 Input size와 동일한 4x4로 만드는 것이다. 이를 위해 양 변에 transposed C(Ct)를 곱해준다. 수식으로는 Ct x C x X = Ct x Y이다. 우변의 Ct x Y를 표현한 것이 아래 그림이다. 결과 형상은 16x1인데, reshape하면 4x4 결과를 얻을 수 있다. 이 결과는 convolution하기 전 상태인 Input(X)과 동일한 결과를 내는 것이 아니다. convolution한 필터(C)를 그대로 사용한다고 해도 deconvolution의 결과는 Ct x C x X이다.
이 블로그를 참고하면, 위의 matrix 연산보다 deconvolution에 대한 직관적인 이해에 도움이 될 것이다.
4. Skip Architecture

Figure 2의 고양이 히트맵을 Upsampling한다고 상상해보자. 그래도 Figure 1의 Segmentation g.t.와 근사한 Output이 나올 것 같지 않다. 히트맵의 정보가 부족(Coarse)하기 때문이다. Convnet 연산이 진행될 수록 feature map은 점점 추상화되고, 정보가 소실돼 input 이미지의 모든 정보를 담을 수 없다. Figure 4의 FCN-32s도 FCN의 마지막 레이어만을 사용한 Segmentation 결과인데, Ground truth와 얼추 비슷하긴 하지만, 정확한 경계를 예측하는 Localization이 빈약하다는 것을 확인할 수 있다. 아직 뭔지는 모르겠지만, FCN-16s와 FCN-8s이 더 정확하게 Segmentation 했다.
좋은 Semantic Segmentation은 semantic(클래스 분류)과 location(클래스의 정확한 위치 정보)을 잘 추론해야 하지만, 고양이 히트맵이나 FCN-32s 결과는 Semantic에만 치중되어 있다고 본다. Lower layer(Input 이미지에 가까운 층)의 feature map은 shallow, fine, appearance, local information을 담고 있고, Higher layer(Output에 가까운 층)의 feature map은 deep, coarse, semantic information을 담고 있다. 이는 layer의 깊이에 따른 상대적인 개념이다. 이런 관점에서 Highest layer의 Output만 이용하는 것은 dense semantics와 coarse location을 이용한다는 것이다. FCN 논문에서는 location 문제를 해결하기 위해 Skip Architecture를 사용했다.
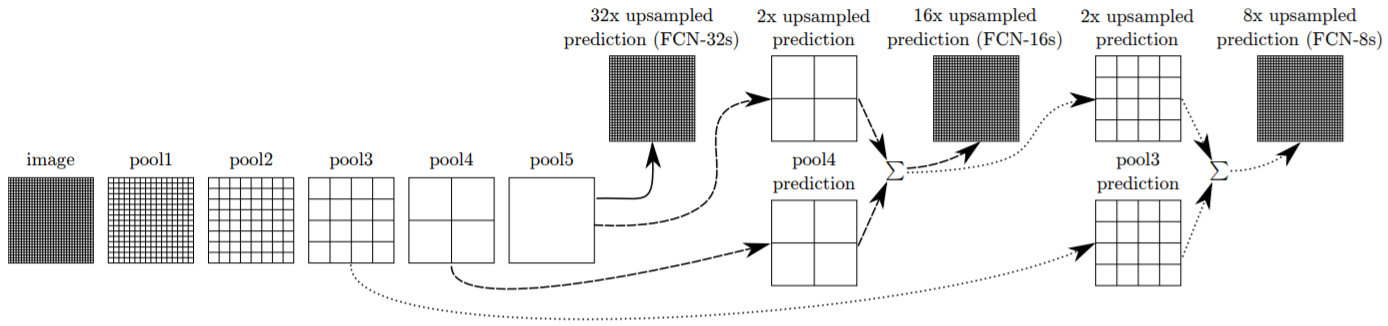
Skip Architecture의 기본적인 개념은 Lower layer의 feature map도 추론에 사용하겠다는 것이다. 앞서 FCN-16s, FCN-8s가 FCN-32s보다 segmentation 결과가 좋았는데, FCN-16s와 FCN-8s는 중간 레이어의 Output도 이용했기 때문이다. Figure 3에 Skip Architecture가 명확히 표현되어 있다. Figure 3은 image가 pooling을 거치면서 1/2 downsample되고, 총 5개의 pooling layer가 있는 예시다. 따라서 5번째 pooling의 결과를 처음 사용했던 image와 같은 사이즈로 만들어 주기 위해서는 32배(2**5) Upsample 해주어야 한다. 이렇게 pool5의 결과만 이용한 것이 FCN-32s이다. FCN-16s는 pool5의 결과와 pool4의 결과를 함께 이용하여 추론한다. 먼저 pool5층의 결과를 2배 upsample하여 pool4층의 결과와 사이즈를 같게 만들어준다. 두 층의 prediction을 더한 다음 16배 upsample하면 image와 같은 사이즈의 segmantation map이 나온다. FCN-8s는 같은 방법으로 pool3의 결과까지 함께 이용하는데, pool4와 poo5의 결과를 더한 값을 2배 upsample해 pool3과 사이즈를 같게 한 후, 8배 upsample하여 최종 결과를 구한다.
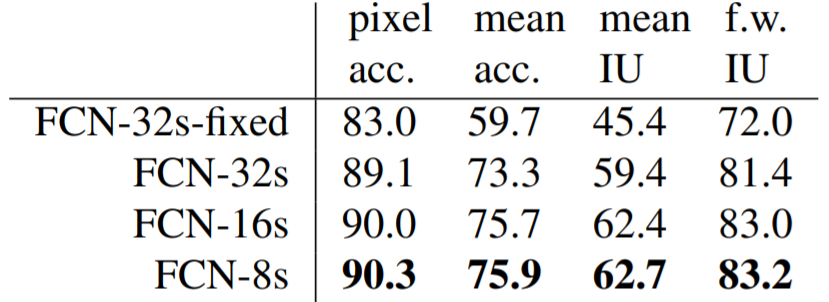
논문에서는 VGG16을 기본 구조로 FCN-32s, 16s, 8s를 학습하여 pixel accuracy, mean accuracy, mean IU, frequency weighted IU을 지표로 성능을 비교하였다. 이미 눈으로 확인했듯이 lower layer를 많이 사용할수록 성능이 높아졌다. 참고로 각 지표의 산출 방식은 아래와 같다.
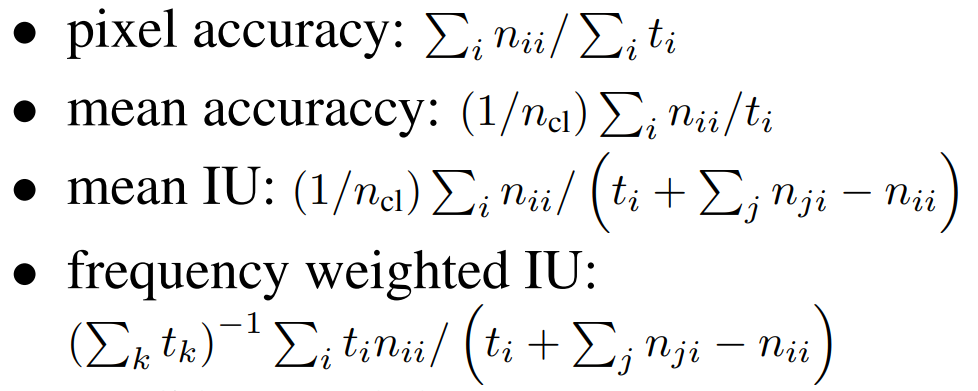
- ncl : 전체 클래스 수
- nij : 클래스 i의 픽셀 중 j 클래스로 예측된 픽셀의 개수.
- ti = ∑j nij : 클래스 i의 전체 픽셀 수
5. Other details
end-to-end network
FCN은 한 흐름으로 Input에서 Output을 도출하는 end-to-end network다. 이와 반대로 여러개의 model을 합쳐놓은 것과 같은 hybrid model이 있으며, hybrid model의 대표적인 예로는 Region Proposal과 Classification을 따로 구현하는 R-CNN 등이 있다.
none patch-wise learning
논문에서는 이미지 단위와 patch 단위로 학습하는 것을 비교한 결과, 이미지를 한번에 학습하는 것이 성능에서는 차이가 안나지만 연산 비용을 따지면 더 효율적이라고 판단했다.
FCN 수식 정의
논문의 Related work를 보면 Fully convolution network 방법을 이 저자가 처음 사용한 것은 아니다. 후에 설명할 Skip Architecture가 본 논문에서 새로 추가한 개념인듯 싶다. Fully convolutional networks란 이름만 보면 신경망 구조가 Convnet으로만 이루어진 모델을 상상할 수 있다. 맞는 말이다. 논문에서는 이 표현을 아래와 같이 표현한다.
While a general deep net computs a general nonlinear function, a net with only layers of this form computs a nonlinear filter, which we call a deep filter or fully convolutional network.
그리고 일반적인 신경망이 비선형 함수를 계산한다면, "이 공식"을 따르는 층으로만 구성된 신경망은 비선형 filter를 계산한다. 이를 우리는 deep filter 혹은 fully convolutional network라고 한다.
- Figure 1 from Fully Convolutional Networks for Semantic Segmentation(2015) -
여기서 "이 공식"이란 아래 두 개의 공식을 말한다. equation 1은 어떤 layer(x)로 그 다음 layer(y)를 계산하는 것을 표현한다. f는 합성곱일 수도, 풀링일 수도 있다. equation 2는 equation 1을 따르는 여러 함수(f, g)를 합성해도 결국 하나의 equation1 함수로 표현되는 것을 보여준다.
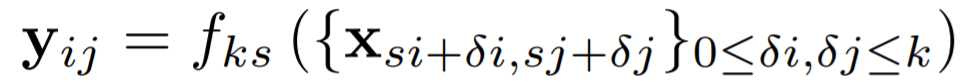

- xij : 어떤 레이어 벡터의 i, j 원소
- yij : x 바로 다음 레이어 벡터의 i, j 원소
- fks, gks : 레이어 타입 (convolution, average pooling, max pooling, activation function and etc)
- k : 커널 사이즈 (정사각 모양 가정)
- s : 스트라이드, subsampling factor
equation 1은 매우 복잡해보이지만, 사실 우리가 알고 있는 합성곱, 풀링 등 필터 연산을 식으로 표현한 것이다. 활성화 함수같은 경우에는 k와 s를 1로 하여 계산하는 것으로 보인다. 아래 그림을 보면 이해가 더 쉬울 것이다. ①에서 ②로 가는 연산을 g, ②에서 ③으로 가는 연산을 f라고 한다면 노란색 화살표은 fks º gk's', 하늘색 화살표는 (f º g)k'+(k-1)s', ss'이다. 여기서 노란색 화살표는 (f º g)k'+ks', ss' 로 표현되는 것 같다. 그래서 아래 그림의 노란색과 하늘색은 정확하게 일치하지 않는다. (f º g)k'+(k-1)s', ss'에서 ②의 초록색 receptive field의 커널 사이즈를 k가 아닌 k-1가 되는 이유를 더 알아볼 필요가 있다.

Any Input size
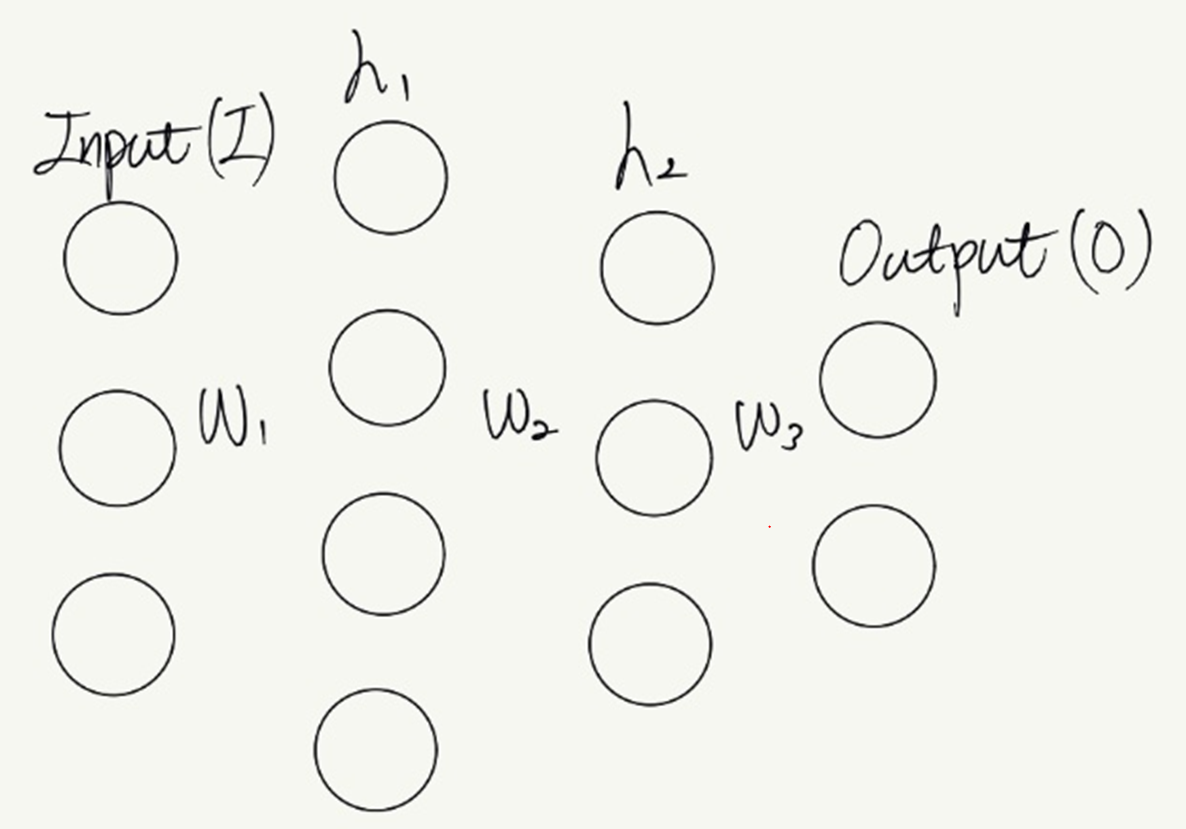
FCN은 처음부터 끝까지 filter 연산(Convolution 연산)만 하기 때문에, input size에 상관않고 작동한다. 반대로 Fully connected layer(FC)를 사용하면 input size가 고정되야 한다. FC를 연결하는 weight size는 앞, 뒤 layer의 노드 수에 따라 정해진다. FC로만 이루어진 신경망의 경우 input size는 첫번째 층의 weight size에 영향을 미친다. 즉, input size가 고정되어야 첫번째 층의 weight size도 고정된다. 아래 3층 신경망 예시는 각 층의 노드 수에 따라 weight size가 다음과 같이 정해진다. W1 = (3x4), W2 = (4x3), W3 = (3x2). 기존 Image recognition 모델도 이미지 input size가 고정되어야, 분류기(FC)에 들어가는 feature map의 크기(분류기의 input size)가 고정된다. 따라서 학습시 고정된 이미지 size를 이용해야 한다.
Reference
[1] Fully Convolutional Networks for Semantic Segmentation(2015)
[2] ImageNet Classification with Deep Convolutional Neural Networks(2012)
[3] Going Deeper with Convolutions(2014)
[4] VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION(2014)



