개인정보보호 등 데이터 규약이 발전함에 따라서 사전학습된 모델(PM; Pre-trained Model)에서 규약에 저촉되는 데이터 혹은 정보를 삭제해야 하는 경우가 생겼습니다. 학습한 데이터를 모델이 잊어버리게 만드는 분야를 Machine Unlearning이라고 합니다.
Machine Unlearning은 특정 클래스의 모든 정보를 삭제하는 Class-wise method와 특정 데이터 포인트의 정보만 삭제하는 Instance-wise method가 있습니다. 기존의 방법이 PM에서 정보를 완전히 삭제하는 것을 목표로 두어 실패했다고 하며, 이 논문에서 제안하는 방법은 삭제 대상 정보를 잘못 예측(분류)하도록 유도하는 것입니다.
Machine Unlearning에서 또 다른 문제는 남겨야 하는 데이터 정보도 잊는 것입니다. 잘못 예측하도록 유도하는 방법은 구체적으로 Adverserial Examples와 Instance-wise unlearning입니다. 삭제 대상 데이터와 PM만 이용하며, 모델을 모델을 수정하지 않기 때문에 남겨야 하는 정보를 최대한 보존했다고 합니다.

논문의 Main Figure로 틀을 잡아보겠습니다. Figure 1의 위쪽(Top) 그림은 Adverserial Dataset을 이용해 기존의 Decision Boundary는 유지하면서 삭제 대상 데이터(Df)를 잘못 예측(Misclassify)하도록 유도합니다. 아래쪽(Bottom) 그림은 신경만 중 삭제 대상 데이터를 분류하는데 영향이 큰 가중치를 바꿔 잘못 예측하도록 유도합니다.
Instance-wise Unlearning
구체적으로 살펴보겠습니다. Instance-wise unlearning을 위해 ①삭제 대상 데이터(Df)를 모두 잘못 분류하게 하거나, ②다른 특정 클래스로 분류하게 합니다. Loss 함수의 구성을 보면 ①을 위해 정답을 고르는 확률이 높을수록 Loss를 높게 줍니다. ②는 다른 클래스로 분류할 확률이 높을수록 Loss를 낮게 줍니다.

만약 보존해야하는 데이터(D_{r})를 사용할 수 있다면 삭제 데이터(D_f{)}에 대한 Unlearning Loss와 보존 데이터(D_{r})에 대한 Cross-Entropy Loss를 더한 Loss 함수를 사용해 최적 모델을 만들 수 있습니다. D_{f}에 대한 정보는 잊고, D_{r}에 대한 정보는 보존할 수 있는 것이죠.

하지만 현실에서는 Storage 비용 등으로 D_{r}을 모두 사용할 수 없는 경우가 있습니다. 이런 경우에도 D_{r}에 대한 정보를 보존하기 위해 논문에서는 Regularization Term을 추가하고, Adverserial Example과 Weight Importance를 이용하는 두가지 방법을 제시합니다.
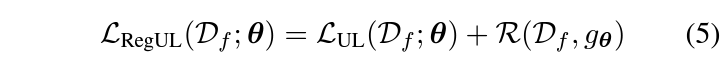
Regularization using Adverserial Examples
삭제 대상 데이터(D_{f})가 N_{f}개 이미지로 구성되어 있다고 가정하면, 이미지마다 PGD attack을 이용해 Adverserial Example을 N_{adv}개 만큼 생성합니다. 이렇게 생성한 이미지 $\bar{D_{f}} = (x'^{(i)}_{f}, \bar{y}^{(i)}_{f})^{\bar{N_{f}}}_{i=1}$ 는 원본 이미지의 타겟값과 다른 타겟값으로 라벨링합니다. 그리고 Regularization Term으로 $\bar{D_{f}}$에 대해 Cross Entropy Loss을 사용합니다. Figure1의 위쪽(Top) 그림에 해당하는 내용으로 $\bar{D_{f}}$의 타겟값은 기존 Decision Boundary를 유지하도록 라벨링됩니다.

Regularization with weight importance
MAS를 이용해 D_{f}에 대한 PM($g_{\theta}$)의 Weight Importance($\Omega^{l}$)를 구합니다. $\Omega^{l}$은 $l$번째 layer의 가중치를 0과 1 사이 값으로 정규화한 값입니다. Regularization Term으로는 각 파라미터마다 업데이트될 변화량에 $ \bar{\Omega}^{l} = 1-\Omega^{l}$를 곱한 값을 사용합니다. 아래 수식에서 $i$는 개별 파라미터를 의미하고, $\tilde{\theta}$는 unlearning 전의 초기 파라미터 값입니다.
