아래 강의 영상의 내용을 정리했습니다.
Bagging
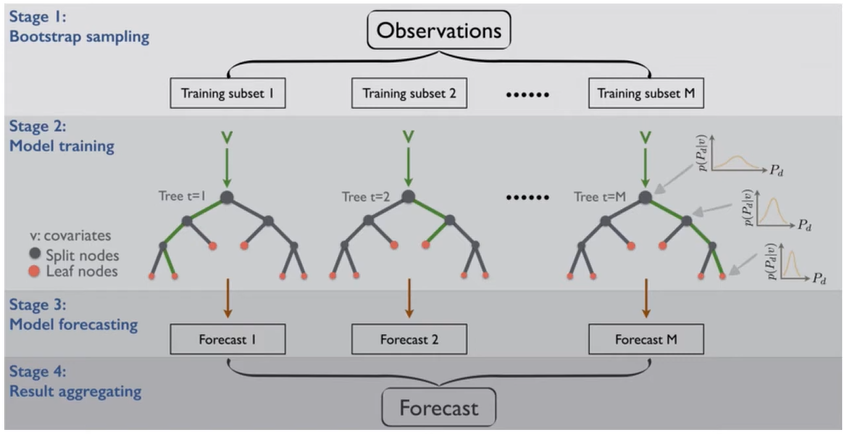
- Bootstrap(복원 추출)을 통해 N개의 Sub Train Set을 구성
- 복원 추출이기 때문에 Sub Train Set에는 동일한 데이터가 2개 이상 뽑힐 수 있음
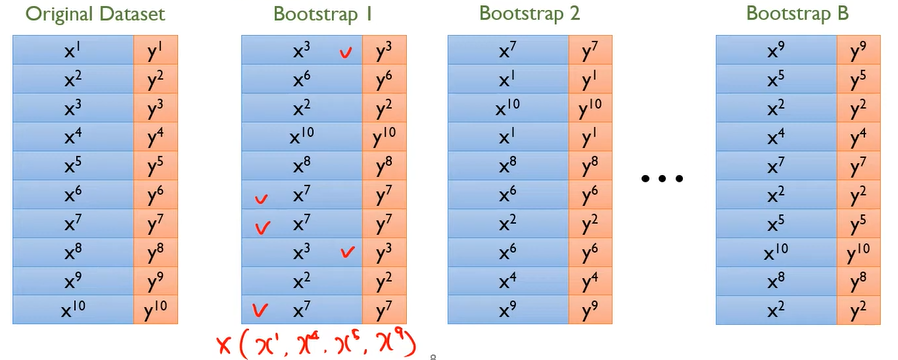
- N이 크다면 2/3는 Sub Train Set으로 뽑힐 것 1/3는 뽑히지 않을 것 → OOB(Out of Bag) 데이터
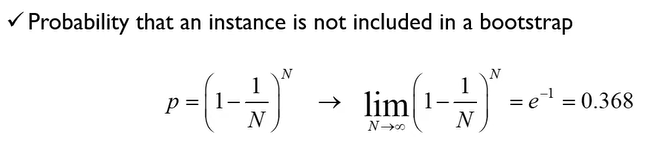
- OOB 데이터를 검증(Validation)에 사용한다. B1으로 M1 학습 → OOB1으로 검증 B2로 M2 학습 → OOB2로 검증 B3로 M3 학습 → OOB3로 검증
- 예측할 때는 베이스 모델의 Output을 합친다.(Aggregation)
- Majority Vote : 베이스 모델의 예측 중에 가장 많은 예측 값을 최종 선택
- Sum prob : 베이스 모델이 예측한 값(0 or 1)의 확률 값을 각각 더해 비교
- Weighted Sum : OOB1, 2, 3로 검증한 성능을 가중치를 그대로 사용하거나, 예측 확률과 곱해 비교
- Stack : 베이스 모델의 Output(클래스별 확률값)을 Input으로 받아 최종 결과를 예측하는 모델을 새로 학습

- High Bias, Low Variance한 모델, 즉 복잡도가 높은 모델과 잘 맞는다 ex) NN, Decision Tree, SVM
Random Forest
- Bagging의 특수한 형태
- Base Model로 Decision Tree만 사용
- 모든 변수를 사용하지 않고 분기할 때마다 Random Sample한 일부 변수만 사용
- 일부 변수만 사용하는 것의 직관적 해석
- 일부 변수만 사용한 Decision Tree는 모든 변수를 사용할 때보다 성능이 낮을 것
- 하지만 Aggregation하면 성능은 높아진다. (직관적 이해)아래 표에서 A반 학생의 평균 점수가 B반 학생의 평균 점수보다 약 10점 높지만, 만약 반 학생들끼리 같이 푼다면 과목별 MAX 점수의 평균은 B반이 훨씬 높다.

Generalization Error
- Pruning(가지치기)을 하지 않기 때문에 개별 베이스 모델(DT)는 오버핏될 가능성이 높다.
- 만약 베이스 모델(DT)의 수가 충분히 많다면, 일반화 오류는 다음과 같다.$\bar{\rho}$ : 베이스 DT 간 correlation coefficients의 평균 → 베이스 DT가 서로 독립적일 수록, 일반화 오류의 상한은 낮아진다.
$Generalization\;Error \leq \frac{\bar{\rho}(1-s^2)}{s^2}$
- $\bar{\rho}$ : 베이스 DT 간 correlation coefficients의 평균 → 베이스 DT가 서로 독립적일 수록, 일반화 오류의 상한은 낮아진다.
- $s^2$ : 마진 (이진 분류인 경우 0과 1 예측 확률의 차이 평균) → 베이스 DT가 정확할 수록 $s^2$는 커지고, 일반화 오류의 상한은 낮아진다.
Example
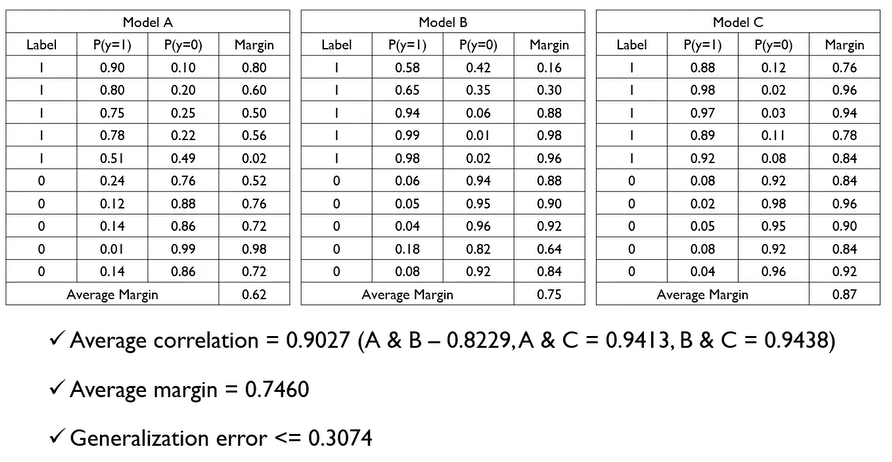
Variable Importance
- 원본 OOB 데이터로 $m$번째 Tree 에러$e_i$를 구한다.
- OOB 데이터의 변수 $i$를 뒤섞은(permute) 다음 $m$번째 Tree 에러$p_i$를 구한다.
- Permute 전후 차이를 구한다.
$$ d_i^m = p_i^m - e_i^m $$ - 전체 Tree에 대해 OOB error 차이의 평균과 분산을 구한다.
$$ \bar{d_i}=\frac{1}{m}\displaystyle\sum_{i=1}^md_i^m, \quad s_i^2 = \frac{1}{m-1}\sum_{i=1}^m(d_i^m-\bar{d_i})^2 $$ - i번째 변수 중요도
$$ v_i=\frac{\bar{d_i}}{s_i} $$
* 변수 중요도의 수치는 상대적인 비교에 사용한다. 절대적인 값이 갖는 의미는 없다.